The ASVAB Mathematics Knowledge section tests your knowledge of a wide range of math topics, concluding with algebra and geometry. It comes in two versions: computerized (CAT-ASVAB) and paper-and-pencil (CAT-ASVAB). The CAT ASVAB math test consists of 16 questions and takes 20 minutes to complete. In the paper-and-pencil version, you have 24 minutes to answer 25 questions.
Calculators are not authorized in the Mathematics Knowledge part. The best way to prepare for the test is to familiarize yourself with as many Math Formulas for the ASVAB as possible. This test’s score contributes to your AFQT score and affects your percentile rank directly. Make sure you’re completely prepared for this section before taking the real test. To fully prepare for your next exam, take more of our ASVAB practice test or read more of our ASVAB Study Guide for all 9 ASVAB parts.
What Kind Of Math Is On The ASVAB?
Our ASVAB Math study guide encompasses the simple to complex nature of mathematically-inclined concepts including fractions, percentages, certain math properties, basic algebra, exponents, and logarithms. Do take your time to thoroughly read each topic and understand the given examples.

Fraction
Multiplication of Fractions
Try to recall these simple fractional terms:

Where the variable above the fraction is called the Numerator and the variable below is called the Denominator.
To try this out, let’s try multiplying these fractions:
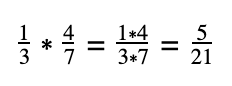
We first multiply the numerators and then the denominators to find the answer.
Take Note:
Try to always reduce the result to its lowest possible terms. Given this example, both the numerator and denominator don’t have common factors thus, this fraction can no longer be reduced.
Division of Fractions
For example:
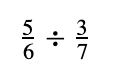
This can be done by changing the division sign (÷) into a multiplication sign (×) and then reciprocating the second number.
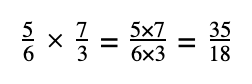
Like the example given above, this case cannot further be reduced.
Mixed Fractions
A fundamental way to deal with mixed fractions is by turning them into an improper fraction which is a different kind of fraction that has a greater numerator than the denominator.
Supposed that we have this mixed fraction:
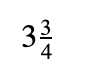
We can convert it through the multiplication of the whole number(3) with the denominator(4) and subsequently, adding the product of the latter with the numerator( 3).
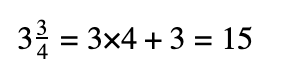
As a result, the denominator from the first mixed fraction will be the same as the improper fraction.
Improper to Mixed Fraction Conversion
As we see from the preceding examples, we’ve converted a mixed fraction (known as a mixed number) to an improper fraction. But now, we’ll learn about the reciprocal of the matter.
Let’s try this example:
12/7
We can simply convert it by dividing the numerator by the denominator.
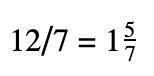
Meaning, we first divide 7 by 12 resulting in 1 then bring down 5. After this, you’ll put the remainder which is 5 beside the quotient (1) in a fraction manner as a numerator and retain the denominator which is 7.
Percentage
The percentage formula is utilized when expressing a number between one and zero. More so, it is used to know the parts of a whole in a more specific way. Denoted with the symbol (%), it is primarily used to determine and compare the ratios.
Percentage(P) = (IV ⁄ TV) × 100, where IV is the initial or pre-given value and TV is the total value.
Sample problem:
In a singing competition, there are 20 contestants. Out of them, 11 are boys. Determine the percentage of boys in the said contest.
Solution:
Total number of contestants in the class = 20
No. of Boys in the competition = 11
% of boys in the competition = (11 ⁄ 20) × 100 = (1100 ⁄ 2000) = 0.55 or 55%
Read more >> Free ASVAB Auto and Shop Information Study Guide 2025
Basic Properties of Numbers
Generally, there are four properties of numbers: associative, commutative, identity, and distributive. Such properties are important rudiments upon advancing to a higher level of mathematics.
Associative Property
Addition: When two or more numbers undergo addition or multiplication, regardless of the way they are arranged, the sum will remain unchanged.
5 + (4 + 1) = 10 or (5 + 4) + 1 = 10
Commutative Property
Multiplication. When two numbers undergo multiplication or addition, regardless of their group, their product or sum remains the same.
8 x 6 = 48 or 6 x 8 = 48
Identity Property
1. Addition and Subtraction. The sum and difference, respectively of any value with zero being that number
5 + 0 = 5 , 5-0=5
2. Multiplication and Division. The product and quotient of any value with one being that number.
15 x 1 = 15, 15/1= 15
Distributive Property
This property entails the solution in an expression such as a(b + c) or literally following the PEMDAS rule.
3 x (4 + 5) = 27 or 3 x 4 + 3 x 5 = 27
Algebra
It is the study of mathematical symbols along with rules encapsulating variables with distinct contexts and is also referred to as the backbone of mathematics.
Solving for x in a Basic Equation
Oftentimes, we get to solve x in every exam or test given by our teacher or professor. Basically, the main objective is to get the value of x through ‘reverse PEMDAS manipulation. In other words, whatever is done on the left side, will also be performed on the right side of the equal sign.
Sample Problem:
x + 7 = 10
With this, we are trying to determine the possible x value that when subtracted to 7, will have a difference of 10. This may be logically easy but we’ll try getting the x value by itself. For that to happen, we have to remove 7 from the left side by subtracting 7 on both sides.
x + 7 = 10
x + 7 – 7 = 10 – 7
x = 3
Determining the x value in an Inequality Equation
The solving process in finding x is similar to an inequality. One thing that differs is that, through division or multiplication by a negative value, the direction of the inequality’s sign changes.
Sample Problem:
2x + 20 ≥ 40
Like equality’s first step, we start by subtracting 20 on both sides.
2x + 20 ≥ 40
2x + 2 −20 ≥ 40 −20
2x ≥ 20
After that, we then divide 2 into both sides. The inequality’s direction remains unaffected due to the fact that we’ve divided it with positive value.
x ≥ 10
Exponents
Generally, it involves two numbers and is used when multiplying a number by itself. More so, it is stated as “a raised to the power of n” or aⁿ.
One example is, 6 cubed:
6^3
= 6 x 6 x 6
= 216
Next example, 7 squared:
72
= 7 × 7
= 49
Take note:
A value raised to the power of 1 equals itself such as 51= 5 x 1= 5, itself
A value raised to the power of 0 equals 1 such as 70 = 1
You can simply subtract the exponents whenever the base is the same such as
95 / 93
= 95-3
= 92
To check:
95 = 9 x 9 x 9 x 9 x 9 and 93 = 9× 9× 9
95 / 93 = (9 x 9 x 9 x 9 x 9) / (9 x 9 x 9)= 9 × 9 = 92
Square Roots
To put it simply, the square root is the mathematical inverse of taking a square root, meaning —square root “nullifies” squared values.
Let’s try, 4 squared or 42
42 = 4 × 4 = 16
To put it into perspective, we can figure out what number is necessary to be squared when we successfully determine the square root of a given number,
Advice: Try asking yourself, “What numerical value squared could give us the given value such as 16?”
Logarithm
Logarithm denoted as log(x) serves as the function in contrast to exponentiation, and is referred to as the power to which a given value must be raised to obtain the necessary rate. It is widely known as a math operation that figures out the frequency or number of times a certain value termed a base, undergoes multiplication by itself. It is also used in various statistical methods that track arithmetic processes in a particular mathematical context.
Common Logarithms
Mathematically, these are types of logarithms limited to base 10.
Also written as:
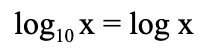
Natural Logarithms
It is a special form of logarithm in which the base is a constant e, where e is an irrational number. The natural log of a number x is written as:
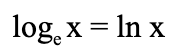
Take note that, ln is the inverse of e.
Negative Logarithms
Logarithms don’t usually settle with negative values but this serves as an exemption, such that all values situated between 0 and 1 are deemed as negative algorithms.
ASVAB Math Help FAQs
Is the ASVAB math hard?
According to recent studies, the mathematics knowledge test is the most difficult ASVAB subtest. Read carefully our free ASVAB Math study guide to get a better understanding as well as strategies and tricks for getting the highest ASVAB scores in this section!
What grade math is ASVAB?
The ASVAB Mathematics Knowledge portion will assess your knowledge of basic high school mathematics. This information would be covered in your 10th-grade math classes and prior grades, such as basic Algebra and basic Geometry.
What if I fail math on ASVAB?
If you fail the test the first time, you can retake it after only one month. If you don’t do well on the second try, you can retake it after another month. Your fourth and subsequent attempts will require a 6-month wait from the previous test.
Are you allowed a calculator in ASVAB Math?
One of the ASVAB standardization requirements is that no calculators be used while taking the tests.
Can I fail the ASVAB arithmetic and math sections and still get a high score?
No. The AFQT (Armed Forces Qualification Test) score is the sum of the 2 math and 2 verbal sections. To be eligible for the army, you must have a minimum score of 31.
How Many Math Questions Are On The ASVAB?
The Mathematics Knowledge test (CAT-ASVAB) has fifteen questions and a time restriction of 23 minutes, but the paper-and-pencil version (P&P-ASVAB) has twenty-five inquiries and a time limit of 24 minutes.
Conclusion
Finally, this ASVAB Math Study Guide is a must-have resource for anyone hoping to ace the mathematics component of the Armed Services Vocational Aptitude Battery (ASVAB). This study guide can help you improve your score and reach your military goals by providing a full review of all the math subjects covered on the ASVAB, as well as numerous practice questions and useful advice. By devoting time and effort to learning the information in this book, you will be well-prepared to take the ASVAB math test and succeed. So don’t hesitate to get a copy and start studying right away!
Besides, our ASVAB Mathematics Knowledge study guide and free ASVAB math knowledge practice test will help you understand the issues completely. You are welcome to take our practice test as many times as you need to improve your knowledge and confidence.




