A 2024 Complete ASVAB Arithmetic Reasoning Study Guide

The ASVAB Arithmetic Reasoning test evaluates a candidate’s ability to solve word problems and provides mathematical questions and equations. These questions may include not only simple addition, subtraction, multiplication, or division, but also reasoning skills to determine what is truly being asked for and the best answer.

The computerized version of the CAT-ASVAB has 15 questions and takes 39 minutes to complete; the paper-and-pencil version has 30 questions and takes 36 minutes to complete. In addition to this ASVAB Arithmetic Reasoning study guide, we offer hundreds of ASVAB practice questions and ASVAB practice test 2024 to help you familiarize yourself with the test format. Let’s give it a try!

ASVAB Arithmetic Reasoning Concepts

The following arithmetic concepts are included in your exam:

• Arithmetic: This concentrates on basic arithmetic such as addition, subtraction, division, and multiplication.
• Percentages:  This kind of question relates to calculating cost price, sale price, discount, etc.
• Ratio and proportion: Ratio/proportion-related questions are solved by using simple formulas.
• Interest:  Interest-related questions may require more complicated formulas.
• Numbers: This asks for your knowledge of whole numbers, decimals, real numbers, fractions, imaginary numbers, etc.

The Arithmetic Reasoning section is used to calculate your Armed Forces Qualification Test (AFQT) score so you should get a good score on this section. Take our Arithmetic Reasoning ASVAB practice test as much as possible to familiarize yourself with the test format and determine your strengths and weaknesses. 

These word problems may have some technical terms, besides basic terms, such as area, perimeter, integer, or ratio, which are expected to be common mathematical knowledge. When solving Arithmetic Reasoning questions, you must pay attention not only to the numbers mentioned in the problem but also to the wording, the format of the paragraph, buzzwords, and more.

ASVAB Arithmetic Reasoning Tips and Tricks

Finding “buzzwords”

These words or phrases of emphasis indicate the action you will need to solve the problem. For example, if a problem mentions “difference”, “fewer” or “take away”, it may require you to use subtraction, while some words like “times”, “product” or “double” may stand for multiplication. Before solving the problems, make sure you carefully read and identify what process it requires. It will show you the direction you should take to solve the overall equation.

Identify numbers

Word problems can be simple with an addition or subtraction of 2 numbers, or they can include more complex numbers and operations. Pay attention to all the given numbers and figures within the body of the paragraph. Read carefully these numbers, and then determine which of the numbers are relevant to solve the problem and which of them are misleading you. 

Make sure you perform them in the right order. 6 – 8 and 8 – 6 bring two very different results and may affect your pass or fail. Be as careful as possible with the number to avoid unnecessary mistakes. 

Paragraph Format

When dealing with the Arithmetic Reasoning section, you should notice that many word problems may contain irrelevant information that is used as a filler to distract you from the real question being asked. You must learn to scan all over the problem, disregard this misleading verbiage, and focus on the portions that will help you answer the problem. Just because something is included in a paragraph doesn’t mean that it is important and must be used.

By identifying the format and context of the paragraph combined with the buzzwords and numbers, you can build a completed, simplified equation. Be sure that you select all the necessary information, make a proper equation, and solve it. 

If you run into a problem that stumps you, skip it to move ahead to another one and then come back to it if you have time. Do not waste too much time on a problem, try to quickly solve the other questions that you are certain about it.

Steps to Solving ASVAB Word Problems

Here is the suggested route to answer the questions in the ASVAB Arithmetic Reasoning test.

Carefully read the problem

Because of the limited time, you may push yourself to solve a problem quickly. This easily leads to the disaster of failing the test. Word problems can be tricky, so you have to thoroughly read each to identify exactly what is being asked for.

Determine the method used to answer

After thoroughly understanding the problem, you’ll need to gather all the relevant data from the problem and decide what is the best way to solve the question it is asking. 

Setup the equations

Once you have determined the method used to answer, you need to set all the relevant data into an equation that will lead you to the correct answer.

Solve equations and review results

When you have the equations for the question, solve it to find the final result. Then quickly review to make sure there is no regretful mistake in the solving progress. 

Basic Arithmetic Review for ASVAB Exams

Before starting to practice the Arithmetic problems, let’s review all the basic definitions, properties, and Arithmetic Reasoning formulas you may need in the ASVAB Arithmetic.

Types of Numbers

Natural Number

Natural numbers (i.e. counting numbers) are numbers that are used for counting and ordering. They can be expressed mathematically as {1, 2, 3, 4, 5, …}

Even Number

Even numbers are natural numbers that are divisible by 2. 

2ℕ = { 2, 4, 6, 8, 10, 12, 14, … }

Odd Number

Odd numbers are natural numbers that are not divisible by 2. 

2ℕ + 1 = { 1, 3, 5, 7, 9, 11, 13, 15…} 

Prime Number

A prime number is a number greater than 1 that is only divisible by 1 and by itself.

Examples:

2, 3, 7, and 11 are prime numbers

P = { 2, 3, 5, 7, 11, 13, 17, 19,…}

Composite Number

Composite numbers are the product of some prime numbers. For example:

8 = 2 ⋅ 2⋅ 2

10 = 2 ⋅ 5

Whole Number

In mathematics, whole numbers are the basic counting numbers 0, 1, 2, 3, 4, 5, 6, … and so on.

Integers

An integer number includes all positive whole numbers (a positive integer), and negative whole numbers (a negative integer), or zero.

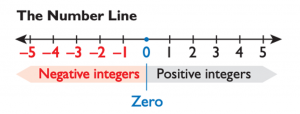
We can put that all together like this:

Integers = { …, −4, −3, −2, −1, 0, 1, 2, 3, 4, … }

Fraction/Rational Numbers

A fraction/rational number is a ratio of two integer numbers in the form of A/B, where A and B are integers and B#0.

A is called a Numerator

B is called a Denominator

Irrational Numbers

Real numbers that cannot be written as the quotient of two

integers but can be represented on the number line.

Example: 

-2√3 , √2, π

Real Numbers

Include all numbers that can be represented on the number line, that is, all rational and irrational numbers.

The Basic Number Properties

Four basic properties of numbers include commutative, associative, distributive, and identity. You should familiarize yourself with each of these before taking the Arithmetic Reasoning subtest.

Properties of addition

Identity Property of Zero: 

a + 0 = a

Inverse Property: 

a + (-a) = 0 

Commutative Property: 

When adding two numbers together, the outcome (sum) is the same regardless of the order the numbers are placed in.

a + b = b + a

For example, the two following equations end up with the same result:

4 + 6 = 10 or 6 + 4 = 10

Associative Property: 

When adding multiple numbers together, the outcome (sum) is the same regardless of the order the numbers are placed in.

(a + b) + c = a + (b + c) 

Properties of subtractions

Non-Commutativity

Unlike addition, the order of two numbers in subtraction changes all the results. In other words, the subtrahend and minuend are distinct factors when subtracting and they cannot be switched order-wise (except subtrahend and minuend are equal).

a – b # b – a

For example :

8 – 6 = 2 is not the same as 6 – 8 = -2

Non-Associativity

When subtracting multiple numbers, the order of the numbers does matter. Subtracting numbers in different orders will result in different outcomes. 

Properties of multiplication

• Property of Zero: 

a × 0 = a

• Identity Property of One: 

a × 1 = a, where a # 0

• Inverse Property : 

a × 1/a  = 1, where a # 0

• Commutative Property: 

When multiplying two numbers together, the product is the same regardless of the order in which the numbers are placed.

a × b = b × a

For example, the two following equations end up with the same result:

2 × 3 = 6 or 3 × 2 = 6

Associative Property :

When multiplying multiple numbers together, the product is the same regardless of the order in the numbers are placed in.

(a × b) × c = a × (b × c)

For example :

(2 × 3) × 4 = 2 × (3 × 4) = 24

Properties of division

Property of Zero: 

0/a = 0, when a # 0.

Property of One: 

a/a = 1 when a # 0. 

Identity Property of One: 

a/1 = a × 1.

Absolute Value

The absolute value of a number is always greater than 0. 

If a > 0, |a| = a. 

If a < 0, |a| = a. 

For example, |8| = 8 and |-8| = 8. In each case, the answer is positive.

Order of Operations 

Step 1: Parentheses – Simplify any expressions inside parentheses. 

Step 2: Exponents (Powers, Roots) – Work out any exponents. 

Step 3: Multiply or Divide before you Add or Subtract

Step 4: Addition and Subtraction These are done last, working from left to right.

For example:

10 – 8 × 4 + (6 ÷ 3) + 5 × 23 

= 10 – 8 × 4 + 2 + 5 × 8

= 10 – 32 + 2 + 40

= 20

>> More: General Science ASVAB Study Guide

Integers

Adding and subtracting with negatives

– a – b = (-a) + (-b)

– a + b = b – a

a – (-b) = a + b 

Example:

– 2 – 3 = (-2) + (-3) = -5

– 2 + 5 = 5 – 2 = 3

2 – (-3) = 2 + 3 = 5

Multiplying and dividing with negatives

-a × b = -ab

-a × -b = ab

(-a)/(-b) = a/b, b # 0

(-a)/b = -a/b, b # 0

Example:

-2 × 3 = -6

-2 × -3 = 6

(-2)/(-3) = ⅔

(-2)/3 = -⅔

Fraction

Fractions are another way to express division. The top number of a fraction is called the numerator, and the bottom number is called the denominator.

Least common multiple

The LCM of a set of numbers is the smallest number that is a multiple of all the given numbers. For example, the LCM of 5 and 6 is 30, since 5 and 6 have no factors in common. 

Greatest common factor

The GCF of a set of numbers is the largest number that can be evenly divided into each of the given numbers. For example, the GCF of 24 and 27 is 3, since both 24 and 27 are divisible by 3, but they are not both divisible by any numbers larger than 3. 

Adding and subtracting fractions

Fractions must have the same denominator before they can be added or subtracted.

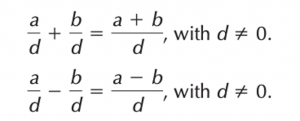
If the fractions have different denominators, rewrite them as equivalent fractions with a common denominator. Then add or subtract the numerators, keeping the denominators the same. For example :

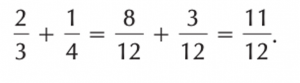
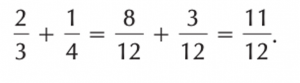
Multiplying and dividing fractions

When multiplying and dividing fractions, a common denominator is not needed. To multiply, take the product of the numerators and the product of the denominators :

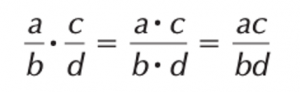
Example :

⅔ × ⅛ = (2 × 1 )/(3 × 8) = 2/24 = 1/12

To divide fractions, invert the second fraction and then multiply the numerators and denominators :

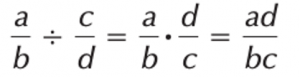
⅔ ÷ ⅛ = (2 × 8)/(3 × 1) = 16/3.

Read more >> ASVAB Math Study Guide

What is in the ASVAB Arithmetic Reasoning section?

Your ability to solve arithmetic and math word problems will be tested on the Arithmetic Reasoning subtest. On the computer test, you will be given 15 scored questions and it’s 30 scored questions on the paper and pencil test, but you might also be given tryout questions.

How can you improve your Arithmetic Reasoning skills for ASVAB?

Taking ASVAB practice tests like the ones provided above is one of the best ways to prepare for a high score on Arithmetic Reasoning. These ASVAB practice questions will allow you to answer questions similar to those on the test in a timed environment that is quite similar to the actual test experience.

Hope that the above ASVAB Arithmetic Reasoning study guide helps you grasp all the important information you need for your coming exam!

We hope you find our ASVAB Study Guide 2024 useful in learning everything you need to know for your upcoming exam!