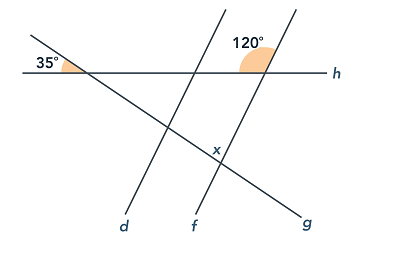
Vertical angles are the angles opposite of each other that are created when two lines cross. Vertical angles are always equal.
So, the angle vertical to the 35-degree angle also has a measure of 35 degrees.
The supplement of the 120-degree angle has a measure of 60 degrees (all straight lines measure 180 degrees), so we then have a triangle with angles measuring 35, 60, and x degrees, as shown in the figure provided.
Since the angles of a triangle add to 180 degrees, x = 180 − 35 – 60 = 85 degrees.